What is a tangent?

February 23, 2023February 24, 2023 / greyessouto / Leave a comment

In simple instances, tangency can be easily characterized. For example, a straight line is tangent to a circle precisely when they share a unique point. More generally, a curve which is the smooth boundary of a convex set has a unique tangent at each point, which can be characterized as the supporting line of the convex set.

But in more general cases such description is inadequate. For example, how do we characterize the tangent to the graph of a polynomial like $y=x^3-6x$ at the point $(1,-5)$ ? The epigraph is not convex, so the description as a supporting line is not available. Also, it clearly intersects the graph at some other point. Even worse, at the point $(0,0)$ the tangent actually crosses the graph, so the latter is not contained in either one of the two half-planes defined by the tangent, even locally. For polynomials, an algebraic definition of tangency in terms of the multiplicity of the point of tangency as a root to a polynomial equation is available, but in more general situations an analytic description is needed.

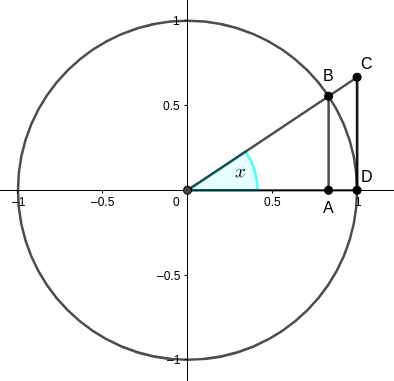
Finding tangents, along with finding areas, is one of the geometric problems that gave impetus to the use of infinitesimals and the eventual creation of Calculus. Predecessors of Newton and Leibniz, notably Fermat and Descartes, devised methods for finding tangents. For example, according to Fermat’s method, to find the tangent to the graph below at $D(x,y)$ , he would choose a point $E(x+h,y(x+h))$ on the graph, very close to $D$ , and would argue that the triangles $\Delta BAD$ and $\Delta BCE$ were “almost” similar. He then wrote an “adequality” (approximate proportion)

$\displaystyle{\frac{|EC|}{|AD|}=\frac{|BC|}{|BA|}}$

or, calling $s=|AB|$ (the subtangent)

$\displaystyle{\frac{f(x+h)}{f(x)}=\frac{s+h}{s}}$ .

This, in turn, can be written as

$\displaystyle{\frac{f(x+h)-f(x)}{h}=\frac{f(x)}{s}}$ .

Expanding and simplifying the left hand side and setting $h=0$ (a predecessor of “finding the derivative”) gives $f(x)=ms$ , $m$ being the slope of the tangent. When $y$ is a polynomial function of $x$ , this program can be easily carried out.

These ideas were further refined by Roverbal, Wallis, Barrow, Newton and Leibniz. The latter defined the tangent as the line through a pair of infinitely close points on the curve.

The modern analytic characterization is the following: the tangent line at a point of a curve has to be such that, as we move along the tangent towards the point of intersection with the curve, the distance to the graph in any “transversal” direction decreases to zero faster than the distance “along” the tangent to the point of intersection. That is, the curve is “transversally” closer to the tangent near the given point. In a sense, the neglect of the transversal separation between the triangles $ABD$ and $CBE$ is the key to Fermat’s construction. The following figure clarifies the situation further.

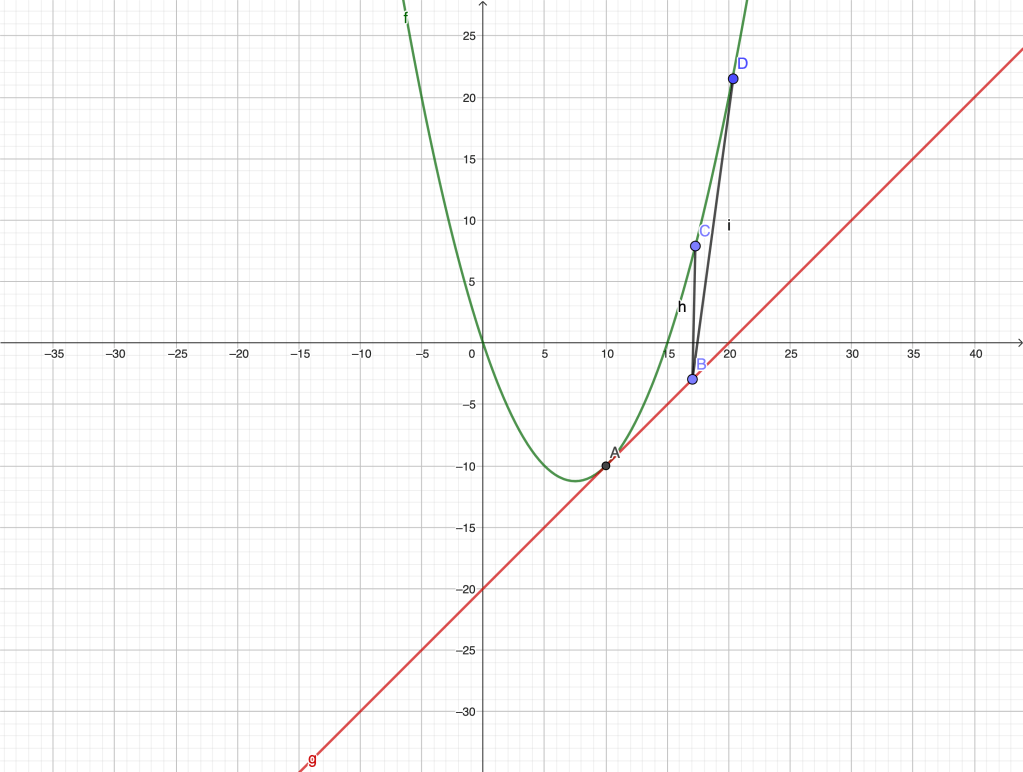
The line $g$ is tangent to the graph at $A$ if

$\displaystyle{|BC|=o(|AB|)}$

when $|AB|$ is infinitesimal. The transversal direction chosen is irrelevant. Had we chosen the direction $BD$ in the above figure, we would still have $\displaystyle{|BD|=o(|AB|)}$ , since as $B$ approaches $A$ , the curve and the tangent become “parallel” and the ratio $|BD|/|BC|$ stabilizes to some positive constant.

Notice that, for a non-tangent, transversal line through $A$ , the ratio $|BC|/|AB|$ is not infinitesimal, but rather stabilizes to a positive value depending on the final non-zero angle between the curve and the chosen non-tangent line.

It follows from our definition that the tangent is unique (if there is one). It is also worth noting that the concept of tangency belongs to Euclidean, as well as to affine geometries: tangency does not break down under rigid motions, translations and more general affine transformations (shear, dilations, etc.)

It is natural to quantify the “amount” of tangency by the order of the infinitesimal $|BC|$ with respect to $|AB|$ . Namely, we will say that the order of tangency is $k\ge 0$ if

$\displaystyle{|BC|=O(|AB|^{k+1})}$

So, in particular, the order of tangency is zero if the line is transversal to the curve, it is one if $|BC|$ is a quadratic infinitesimal, etc. The order of tangency may not be an integer.

Tangents and differentiability

The existence of the tangent to the curve $y=y(x)$ at a point $(x_0,y_0)$ is intimately related to the existence of the first differential $dy(x_0,dx)$ . To see why, we start by noticing that if the curve $y=y(x)$ has a non-vertical tangent at $(x_0,y_0)$ (see figure below), the vertical distance between the graph and the tangent is also infinitesimal with respect to $|AE|$ , because $|AE|$ and $|AB|$ are proportional, $|AE|=|AB|\cos\alpha$ . Therefore

$\displaystyle{\frac{|BC|}{|AE|}=\frac 1{\cos\alpha}\frac{|BC|}{|AB|}\to 0}$

when $|AB|$ is infinitesimal. But $|AE|=|x-x_0|$ , where $x$ is the abscissa of the moving point $B$ .

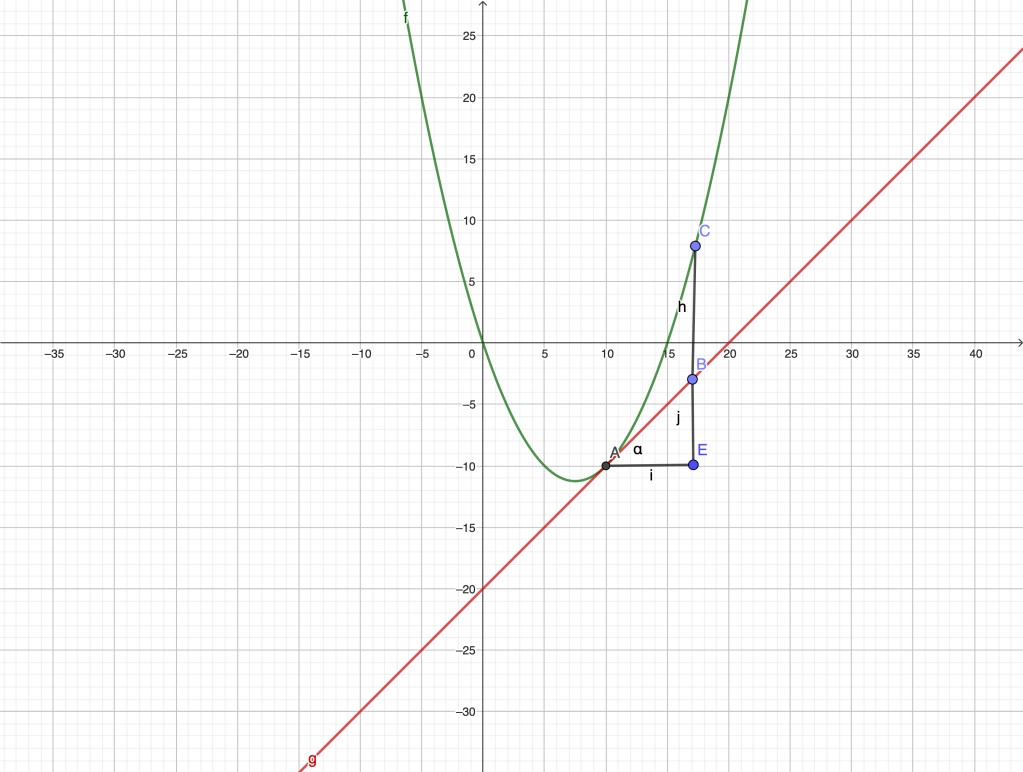
If we assume that the straight line $y=y_0+m(x-x_0)$ is tangent at $(x_0,y_0)$ , we should have

$|BC|=y(x)-[y_0+m(x-x_0)]=o(|x-x_0|)$

$y(x_0+dx)-y(x_0)=mdx+o(dx)$ .

But this is precisely our definition of differentiable function at $x_0$ , with $dy(x_0,dx)=mdx$ . Therefore, the existence of a tangent with slope $m$ implies differentiability with $dy/dx=m$ . The value of the derivative is the slope of the tangent.

If the order of tangency is $k\ge 2$ , that is if

$y(x_0+dx)-y(x_0)=mdx+o(dx^k)$ ,

it follows from the definition that $d^ry(x_0,dx)=0$ for $r\ge k$ .

As an example, let’s examine the order of tangency between a circle and its tangent at some point. For simplicity, consider the circle

$x^2+(y-1)^2=1$

with unit radius, center $(0,1)$ and tangent to the $x$ -axis at the origin $O$ , see the figure below.

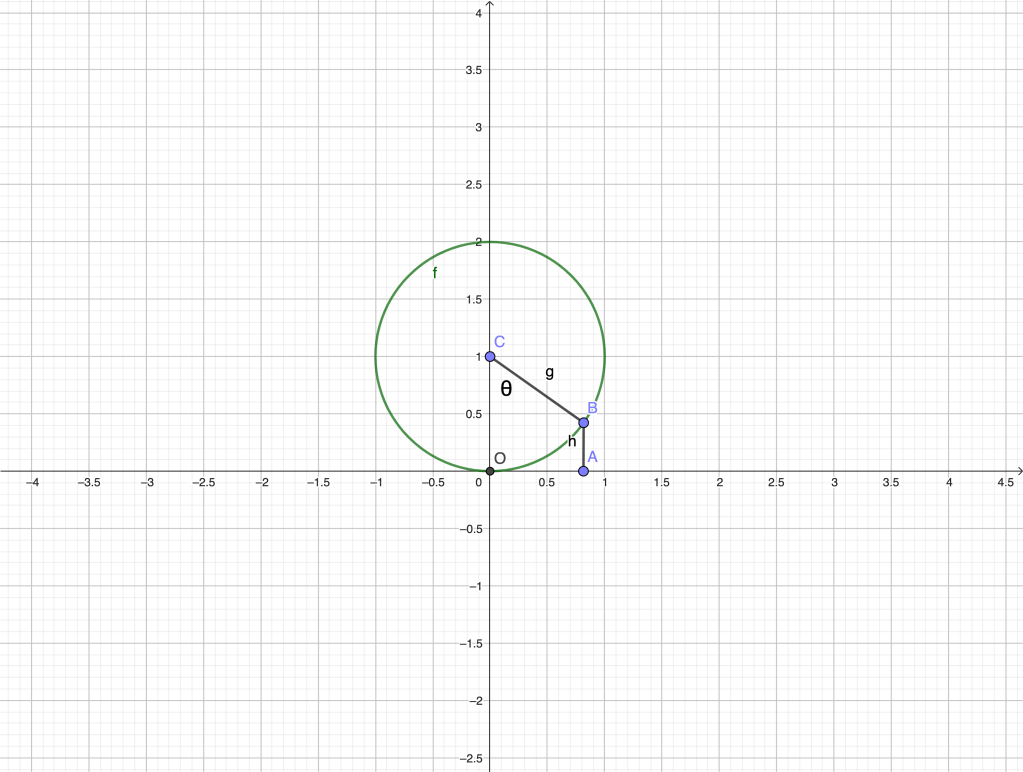
We have $|OA|=\sin\theta$ , $|AB|=1-\cos\theta$ . Therefore,

$\displaystyle{\frac{|AB|}{|OA|}=\frac{1-\cos\theta}{\sin\theta}=\frac{\sin\theta}{1+\cos\theta}\to 0}$

as $\theta\to 0$ . Hence $|AB|=o(|OA|)$ . Actually, $|AB|$ is an infinitesimal of the second order with respect to $|OA|$ . Indeed,

$\displaystyle{\frac{|AB|}{|OA|^2}=\frac{1-\cos\theta}{\sin^2\theta}=\frac{1}{1+\cos\theta}\to \frac 1{2}}\qquad\qquad (*)$

as $\theta\to 0$ . Thus $|AB|=O(|OA|^2)$ and the order of tangency is $k=1$ .

The value of the limit $(*)$ would be different for circles of different radii. Indeed, if our circle was $x^2+(y-R)^2=R^2$ , since the numerator and denominator in $(*)$ scale differently, the limit would be $1/2R$ .

The usual (linear) angle between a circle and its tangent at one point is zero. But our previous analysis allows to quantify the separation between the circle and the tangent using an infinitesimal quadratic scale. Observe that when $R$ is close to zero, $1/2R$ is very large, whereas when $R$ is very large and the circle is “very close” to its tangent, $1/2R$ is close to zero.

Angles like the above, whose usual measure is zero but their extent can be quantified as before, have been known since antiquity.

Horn angles

A horn angle is the angle formed between a circle and its tangent or, more generally, between two tangent circles at their point of tangency. Given two circles internally tangent, it is natural to define the measure of the horn angle between them as the difference of the angles they form with their common tangent. If they are externally tangent, we take the sum instead, as in the figure below.

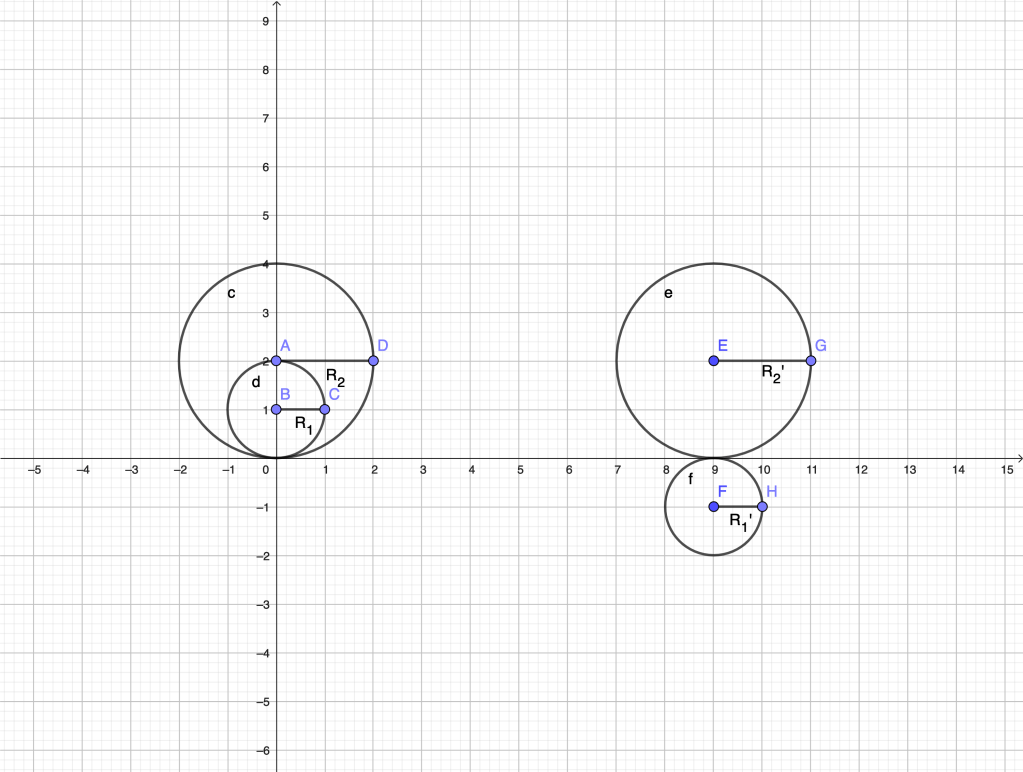
Thus, $\angle (c,d)=1/R_1-1/R_2$ in the first case, $\angle (e,f)=1/R'_1+1/R'_2$ in the second. The factor $\lq\lq 1/2"$ is common and omitted for simplicity. For a circle of radius $R$ , the quantity $1/R$ is called its (scalar) curvature. The measure of a horn angle between two tangent circles is the difference/sum of their curvatures.

Horn angles are mentioned by Euclid in Book III (Prop. 16) of the “Elements”, and were known to Archimedes and Eudoxus. Euclid states that a horn angle is “smaller than any acute angle”. That property made horn angles problematic to Ancient Greek mathematicians, since they always assumed that any two “homogeneous” magnitudes (lengths, angles, areas, ..) were comparable, in the sense that anthyphairesis (as we would say today, the Euclidean algorithm) could be applied to them. At the end of the process, commensurable magnitudes could be assigned numbers with respect to some unit. Incommensurable magnitudes could not, but the situation could be handled by means of Eudoxus’ theory of proportions, a predecessor of Dedekind’s theory of real numbers. But the notion of a non-zero angle smaller than any acute angle was out of grasp. In modern terminology, we would say that the Archimedean property of segments, angles, areas was a basic assumption in Greek geometry.

We have been able to define a measure for horn angles using the concept of order of infinitesimals. However, to restore the Greeks’ assumption on the possibility to compare (albeit “in the limit”) any pair of angles, actual infinitesimal angles of different orders need to be included in the picture. This is the content of non-Archimedean Geometry, based on the construction of non-Archimedean fields (surreal, hyperreal numbers) in Nonstandard Analysis. The development of these ideas is a very interesting chapter of Analysis, well deserving a separate post, or even a separate thread.

Differentials and local power expansions

February 10, 2023 / greyessouto / Leave a comment

In line with the general purpose of this thread, in this post I intend to present a bird’s eye view of the concept of power expansions (Taylor series), in the belief that these ideas are often presented in a highly technical way that makes it difficult for students to grasp their simplicity and significance.

The change of the area of a unit square corresponding to a change $dl$ of its side equals

$\Delta A:=A-1=2dl+(dl)^2$

The linear part of the change is called the first differential of $A$ (to be precise, the first differential of $A$ at the point $l=1$ , corresponding to a change $dl$ of the independent variable). It is denoted by $dA$ :

$dA=2dl$

Thus,

$\Delta A=dA+(dl)^2\qquad\qquad (*)$ .

At this point, the above relation is exact and is valid for any finite $dl$ . However, if we consider an infinitesimal $dl$ , the main contribution to $\Delta A$ is given by the linear (in $dl$ ) part $dA$ , the difference being an infinitesimal of higher order. This observation suggests the following definition: if a function $y=f(x)$ of a variable $x$ is such that

$\Delta f(x,dx)=C(x)dx+o(dx)$ ,

for infinitesimal increments $dx$ , we say that $f$ is differentiable at $x$ . We define the first differential to be $dy=df(x,dx):=C(x)dx$ . The coefficient $C(x)$ is what we call the derivative of $f$ at the point $x$ . Therefore, the derivative is a ratio of differentials, $C=dy/dx$ . Finding the derivative from the knowledge of $y(x)$ involves, in the general case, considering $dx$ and $dy$ infinitesimal (see below). For polynomials, however, it only requires algebraic manipulations.

For example, let us compute the derivative of $y=x^3+2x^2+x-1$ at a generic $x$ . We have to increase $x$ by $dx$ and compute the corresponding change of $y$ :

$\Delta y=(x+dx)^3+2(x+dx)^2+(x+dx)-1-[ x^3+2x^2+x-1]=$

$=3x^2dx+3x(dx)^2+(dx)^3+4xdx+2(dx)^2+dx=$

$=(3x^2+4x+1)dx+(3x+2)(dx)^2+(dx)^3\qquad\qquad (**)$

The linear part is

$dy=(3x^2+4x+1)dx,$

while the rest are quadratic and cubic terms, all of them infinitesimals of higher order, negligible w.r.t. $dx$ . Thus, the derivative of $y$ with respect to $x$ is

$\displaystyle{\frac{dy}{dx}=(3x^2+4x+1).}$

In both previous examples $(*)$ and $(**)$ , the total variations of $A$ (respectively $y$ ) were sums of positive integer powers of $dx$ . That is always the case when considering polynomial functions of $x$ . Namely, if $y=P_n(x)$ is a polynomial of degree $n$ , and we look at the change of $y$ as $x$ is increased from $x$ to $x+dx$ , we will have

$\Delta y=A(x)dx+B(x)(dx)^2+C(x)(dx)^3+\dots W(x)(dx)^n,\qquad\qquad (***)$

with coefficients $A,B,C,\dots W$ depending on the base point $x$ . In order to get $(***)$ , we just expand the powers $(x+dx)^k$ according to Newton’s binomial theorem. We can think of the coefficients as rates of different orders, multiplying the corresponding powers of $dx$ . Thus, we have a clear separation of the factors leading to the change $\Delta y$ : the rates, which depend only on the base point, and the different powers of the variation of the independent variable $dx$ . This is a simple instance of a (finite) “Taylor expansion”. No limit process is involved in the previous computations, and the final expression $(***)$ is exact for any finite value of $dx$ .

One of the main breakthroughs in the development of Calculus is the fact that for non-polynomial functions like $y=\sin x$ or $y=\sqrt{1+x}$ a similar expansion holds. The key difference is that the expansion may contain infinitely many terms. Thus, the concept of a power series serves as a bridge between algebraic and transcendental relations. The idea that (at least smooth) functional relations are either polynomials or “infinite degree polynomials” (power series) dominated Analysis over a long period of time. Newton himself considered the binomial series and the use of series in general to solve differential equations his main mathematical achievement. They also allowed to define many non-elementary functions and to develop Complex Analysis. Series were informally used by Euler, Lagrange, Laplace and many others, in some cases producing paradoxical results. Questions related to convergence were not posed until the middle of the XIX century by Gauss, Abel, Cauchy, etc. It is said that when Laplace heard about Cauchy’s convergence criteria, he rushed home to check the series he used in his monumental “Celestial Mechanics”. Luckily for him and for the stability of the Solar System, all of them were convergent in the range of parameters he considered.

For a relation like $y=\sin x$ , algebraic methods to find the coefficients in the expansion are not available, and need to be replaced by limit procedures. Here is the basic idea: first, we divide throughout by $dx$ , yielding

$\displaystyle{\frac{\Delta y}{dx}=A+Bdx+C(dx)^2+\dots}\qquad (!)$

where the denote $A(x), B(x),$ etc. simply as $A, B,$ etc. As $dx$ approaches zero, all the terms in the r.h.s. vanish except for $A$ . Consequently, $A$ is the limit value of $\frac{\Delta y}{dx}$ . This is how the (first) derivative is usually defined,

$\displaystyle{\frac{dy}{dx}=A=\lim\limits_{dx\to 0}\frac{\Delta y}{dx}.=\lim\limits_{dx\to 0}\frac{y(x+dx)-y(x)}{dx}}$

We can think of successive terms in the right-hand side of $(***)$ as corrections to the previous ones when $dx$ is infinitesimal. Thus, if we only keep the first differential, we obtain the linear approximation of $y$ near $x$ ,

$y(x+dx)\approx y(x)+dy(x,dx)$

which renders a good estimate if $dx$ is small enough, since we are discarding infinitesimals of higher order.

In order to find the coefficient $B$ above, we repeat the procedure. Namely, we take $A$ to the left in (!) and divide by $dx$ again, yielding

$\displaystyle{B= \lim\limits_{dx\to 0}\frac{\frac{\Delta y}{dx}-A}{dx}= \frac{\frac{\Delta y}{dx}-\frac{dy}{dx}}{dx}=\frac{\Delta y-dy}{(dx)^2}}.$

Thus, the infinitesimal $\Delta y-dy$ is typically quadratic, $O((dx)^2)$ or of a higher order, $o((dx)^2)$ if $B=0$ . It is natural that the quadratic correction $B(dx)^2$ is related to the variation of $A$ or, equivalently, $dy(x, dx)$ over the interval $(x,x+dx)$ . Thus, we introduce the second differential of $y$ to measure the variation of the first differential as the base point $x$ changes to $x+dx$ . Namely, we define

$d^2y(x,dx)=d(dy(x, dx),dx)$

where we consider $dx$ a constant and vary the base point $x$ again by the amount $dx$ (this is reminiscent of arithmetic sequences). We have

$dy(x+dx, dx)-dy(x,dx)=A(x+dx)dx-A(x)dx=$

$(A(x+dx)-A(x))dx=G(x)(dx)^2+o((dx)^2)$ ,

and therefore

$d^2y(x,dx)=G(x)(dx)^2$ ,

where $G(x)$ is the derivative of the first derivative $A$ at $x$ . Thus the second differential is quadratic in $dx$ . The coefficient $G(x)$ is called the second derivative of $y$ at the point $x$ The second derivative is thus the ratio of the second differential to the square of $dx$ .

How is $G$ related to $B$ ? The idea is to move along the linear approximation up to $x+dx/2$ and, at that point, use $G(x)$ to “correct” the linear approximation. From the above expression for $B$ ,

$\displaystyle{\frac{\Delta y-dy}{(dx)^2}.=\frac{y(x+dx)-y(x)-Adx}{(dx)^2}=}$

$\displaystyle{=\frac{y(x+dx)-y(x+dx/2)+y(x+dx/2)-y(x)-Adx}{(dx)^2}=}$

$= \displaystyle{\frac{A(x+dx/2)dx/2+B(x+dx/2)(dx/2)^2+A(x)dx/2+B(x)(dx/2)^2-Adx+\dots}{(dx)^2}=}$

$= \displaystyle{\frac{[A(x+dx/2)-A(x)]dx/2+[B(x+dx/2)+B(x)](dx/2)^2+\dots}{(dx)^2}}$ ,

where the dots represent infinitesimals of order higher than $(dx)^2$ . In the limit $dx\to 0$ we obtain

$B(x)=G(x)/4+B(x)/2$ ,

that is, $B=G/2$ .

A completely analogous procedure allows to find $C(x)$ in $(***)$ . This time we need to split the interval $[x,x+dx]$ into three equal pieces, since we want to account for the variation of the second differential, which depends on three points. Precisely, we introduce the third differential of $y$ at $x$ as:

$d^3y(x,dx)=d(d^2(x,dx),dx)$ .

A computation, similar to the one above for the second differential, gives

$d^3y(x,dx)=H(x)(dx)^3$ ,

where $H(x)$ is called the third derivative of $y$ at $x$ . The expression for $C(x)$ is

$\displaystyle{C= \lim\limits_{dx\to 0}\frac{\frac{\Delta y}{dx}-A-Bdx}{(dx)^2}=\frac{\Delta y-dy-\frac{d^2y}{2}}{(dx)^3}}$

A computation similar to the one above gives the relation $C=H/(2\cdot 3)$ . In general, we define the $n$ -th differential recursively

$d^ny(x,dx)=d(d^{n-1}(x,dx),dx)$

and the corresponding $n$ -th derivative $\displaystyle{\frac{d^ny}{(dx)^n}}$ . The total variation of a polynomial of degree $n$ can then be expressed as

$\displaystyle{y(x+dx)=y(x)+dy(x,dx)+\frac{d^2y(x,dx)}{2}+\frac{d^3y(x,dx)}{2\cdot 3}+\dots+\frac{d^ny(x,dx)}{2\cdot 3\cdots n}}$ .

Thus, if we develop a machinery to compute derivatives, we can swiftly write down the expansion $(***)$ for a polynomial, avoiding the use of the binomial theorem and rearrangement. More importantly, transcendental functions like $y=\sin x$ or $y=e^x$ can be dealt with the same way, leading to their power (Taylor) expansions:

$\displaystyle{y(x+dx)=y(x)+dy+\frac{1}{2!}d^2y+\frac{1}{3!}d^3y+\dots+\frac 1{n!}d^ny+\dots}$

For computational purposes, the more terms we keep on the right hand side, the better the approximation for small values of $dx$ . But series expansions are also important for the theory. Many of the usual manipulations with polynomials can be extended to series, including differentiation, integration, long division, etc. In particular, they can be used to solve differential equations with “nice” coefficients.

However, the transition from polynomials to more general functions is non-trivial. We showed above that if the difference $y(x+dx)-y(x)$ can be expressed in the form $A(x)dx+B(x)dx^2+\dots$ , then $y$ has to be a differentiable function of $x$ and the coefficients $A(x), B(x)$ , etc are uniquely determined in terms of the derivatives. The question as to whether such a representation is at all available, even for infinitely differentiable functions, leads to the concept of analytic function, to be considered in a future post.

Differences as precursors to differentials

February 2, 2023February 2, 2023 / greyessouto / Leave a comment

When Leibniz came to Paris in 1672, his mathematical knowledge was rather scant. It was through his acquaintance with Ch. Huygens, one of the leading mathematicians of his time in Europe, that Leibniz’s interest in Mathematics sparked. One of the problems that Huygens proposed was that of finding the sum of the series of the reciprocals of triangular numbers

$\displaystyle{\frac 1{1}+\frac 1{3}+\frac 1{6}+\frac 1{10}+\dots.}$

Realizing that the terms in the series were the successive differences between the terms of the sequence

$\displaystyle{\frac 2{1}, \frac 2{2}, \frac 2{3},\dots.}$

Leibniz concluded that the $n$ th partial sums of the former sequence were equal to the difference between the $(n+1)$ -th term and the first term of the latter, that is $1-\frac 2{n+1}$ (this device is what we call telescoping). He developed this idea, considering sequences of differences of differences (second differences), third differences, etc. Thus, one can move “up” and “down” along the sequence of successive differences, establishing relations between the sums of differences and the net change of the generating sequence.

Perhaps the simplest example is that of arithmetic sequences $\{a_n\}$ . In this case, the sequence of differences is constant, $b_n=a_{n+1}-a_n=d$ . The sum of the first $n$ differences is just $nd$ hence $a_{n+1}-a_1=nd$ or $a_{n+1}=a_1+nd$ . Arithmetic sequences are just linear functions of $n$ .

Now, what if the differences of the original sequence form an arithmetic sequence and the second differences are constant?

Suppose the original sequence is $a_1,a_2,\dots a_{n}$ , the sequence of first differences is $b_1,b_2,\dots b_{n-1}$ where $b_i=a_{i+1}-a_i$ and the sequence of second differences is $c_1,c_2,\dots c_{n-2}$ with $c_i=b_{i+1}-b_i=d$ , a constant. We know that $\{b_i\}$ is an arithmetic sequence with difference $d$ , hence $b_i=b_1+(i-1)d$ . Hence

$a_{n+1}-a_n=b_n=b_1+(n-1)d$

$a_{n}-a_{n-1}=b_{n-1}=b_1+(n-2)d$ ,

$\dots\dots$

$a_{2}-a_{1}=b_{1}$

Adding all the relations above and taking into account the cancelations on the left hand side (telescopic effect) we obtain

$a_{n+1}=a_1+nb_1+d(1+2+\dots +n-1)$

$\displaystyle{a_{n+1}=a_1+nb_1+d\frac{n(n-1)}{2}}\qquad\qquad (!)$

Observe the following: a) $a_n$ is given by a second degree polynomial; b) the free term is the first element of the sequence $a_1$ , the coefficient of the linear term is $b_1$ , the first “first difference”, and the coefficient of the quadratic part is $d$ , which is the constant value of the second difference. At this point it should be clear that we can extend this procedure to the case when the third differences or, more generally, the differences of a certain order $k$ are constant. Unsurprisingly, we get polynomials of degree equal to the order of the constant difference, where the coefficients only depend on the first values of consecutive differences. This is what we could call a “discrete” (and finite) Taylor series.

Leibniz was, above all, a philosopher. He realized that he could extend this methods to functions of a continuous variable. But then he would have to replace the differences by infinitesimal differences between to “successive” values of the variable. He had been thinking about the concept of infinitesimal for years, particularly through correspondence with Hobbes and his concept of “conatus“. All the pieces came together in his mind, leading to the creation of infinitesimal Calculus within a few years. Simultaneously, he introduced the notation for successive “differentials”: $dy, d^2y,$ etc. and integrals (“summa omnia”) $\int, \iint,\dots$ for the above processes of moving “down” and “up”, but this time applied to functions of a continuous variable. The passage $n\to (n+1)$ becomes $x\to x+dx$ . We deal with the continuous case in the next post.

Infinitesimals and their orders

January 7, 2023January 7, 2023 / greyessouto / Leave a comment

Nowadays, we conceive Calculus as the study of functions. The concept of function, originated with Leibniz, was not defined in its full generality until the mid 1800s by Dirichlet. But in the early development of Calculus, the main objects of Calculus were variable quantities, notably those that varied together. For example, Euler considered quantities that vanish or increase infinitely in his famous Introductio in analysin infinitorum, from 1748. Such dynamic view of quantities is one of the features that have been lost or, at least obscured by the modern approach, based on limits. The $\epsilon - \delta$ definition is a bit too “algebraic” and static: the dynamics is encoded in the conditional “ $\forall\epsilon\,\,\, \exists\delta\,\,\,\,$ such that..” Euler’s “quantities”, in contrast, had a variable nature.

A quantity that we can consider as becoming ever smaller is called an infinitesimal. A possible mental image is that of a segment which increasingly diminishes until it becomes a single point, or an angle whose sides become closer and closer until they coincide. In modern terminology, an infinitesimal is a variable whose limit is zero. If a variable quantity $x$ is approaching some (finite) value $L$ , the difference $x-L$ is an infinitesimal.

Calculus is concerned with simultaneous variations of related quantities. Thus for example we can consider the variation of the area of a square of side $l=1$ when its side is increased/decreased by an infinitesimal amount. Such infinitesimal amount was denoted by Leibniz, the Bernoullis, Euler, etc. and even today by physicist, engineers, etc, by $dl$ , and is called a differential. A simple computation gives the new area

$A=(1+dl)^2=1+2dl+(dl)^2$

The corresponding change of area is $A-1$ , which is another infinitesimal. In modern terminology, we say that the area is a continuous function of the side: if the side is infinitesimally increased/decreased, the area changes infinitesimally. In most applications to Physics and Engineering, we deal with continuous functions.

A central idea to Calculus is that infinitesimals can be classified according to the relative speed with which they approach zero. It does not make sense to talk about the speed of one infinitesimal, but it does make sense to talk about whether two related infinitesimals (as the ones considered above) approach zero at a comparable speed. Thus if $h$ is an infinitesimal quantity, the related infinitesimal $h^2$ approaches zero much faster, since their ratio $h^2/h=h$ is itself infinitesimal. We all know that if we look at a sequence of values like $1,0.1,0.01,\dots$ , their squares form a sequence that approaches zero much faster; $1,0.01,0.0001\dots$ . The infinitesimal $h^3$ approaches zero even faster since the ratio $h^3/h^2=h$ is again an infinitesimal.

These considerations lead to the concept of order of infinitesimals. Namely, given two related infinitesimals $h$ and $k$ , we say that $k$ is of a higher order (than $h$ ) if their ratio $k/h$ is infinitesimal. A nice notation introduced by E. Landau and widely used in Computer Science is that of “little o”. Using the “little o” notation, we write

$k=o(h)$

In modern terminology, we would say: given two functions $f$ and $g$ with $lim_{x\to a}f(x)=lim_{x\to a}g(x)=0$ , we say that $f=o(g)$ if $lim_{x\to a}f(x)/g(x)=0$ . This is nice and clean, but one has the impression that the dynamics is somehow lost.

In many instances, two related infinitesimals are “comparable”. Back to the previous example of the area as a function of the side, the quotient

$\frac{A-1}{dl}=2+dl$

is not an infinitesimal, but takes values closer and closer to $2$ instead. In such cases we use the “big O” notation. For generic related infinitesimals $k$ and $h$ as above, we would write

$k=O(h)$

Thus, $A-1=O(dl)$ .

In the particular case when the ratio approaches $1$ , we say that the infinitesimals are equivalent. That means, of course, the given infinitesimals take very close values as they vanish. Equivalency is denotes by the symbol “ $\sim$ “

It seems to me that the qualitative aspect of the concept of order is not sufficiently stressed. Even the suggestive “little o” notation is not used in many of the standard current undergraduate Calculus textbooks, including J. Stewart’s, Edwards & Penney, Larson & Edwards, and many others. I think this is very unfortunate, and is part of a general tendency to avoid “qualitative” and “synthetic” reasoning, favoring quantitave and procedural aspects instead.

An interesting infinitesimal is $y=\sin x$ , where $x$ is an infinitesimal angle. In the figure below, the radius is chosen to be one for simplicity. The following inequalities are obvious.

$Area(OAB)<Area(ODB)<Area(ODC)$

or, equivalently,

$\frac{OA\cdot AB}{2}<\frac{x}{2}<\frac{CD}{2}$

which, after dividing by $AB$ throughout, becomes

$OA<\frac{x}{AB}<\frac{CD}{AB}=\frac 1{OA}$ ,

the latter equality being a consequence of similarity of triangles $OAB$ and $ODC$ .

Clearly, as $x$ approaches zero, $OA$ approaches one. As a consequence. The ratio $\frac x{AB}$ , being trapped between two quantities approaching one, also approaches one. Using the above terminology, $AB$ and $x$ are equivalent infinitesimals, $AB\sim x$ . In the language of limits

$\lim\limits_{x\to 0}\frac{\sin x}{x}=1$ .

A vivid example of infinitesimals of different orders is given by the different segments, areas, etc. determined on a circle by an infinitesimal angle $\theta$ .

When the angle $\theta$ is infinitesimal, the following quantities (functions of the angle): $a, s, h$ and the area of the yellow circular segment are related infinitesimals. $s=R\theta$ is just a linear function of $\theta$ so $s/\theta=R$ which is a non-zero constant. Therefore $s=O(\theta)$ . Next, we see that $a=2R\sin\theta/2$ which, according to the previous example, is equivalent to $2R\theta/2=R\theta$ . Therefore, $a=O(\theta)$ . As for $h$ , we have

$h=R(1-\cos\theta/2)=2R\sin^2(\theta/4)$ .

Since $\sin(\theta/4)\sim\theta/4$ , $\sin^2(\theta/4)\sim\theta^2/16$ and $h=o(\theta)$ .

Finally, the area of the segment is

$A=\frac{R^2\theta}{2}-\frac{R^2\sin\theta}{2}=R^2(\theta-\sin\theta)/2$

On the right hand side, we have the difference between two equivalent infinitesimals. What is the order of that? I will leave the question open at this point, and will come back to it in my next post, where we will deal with successive differences and differentials.

Math Bites

by Guillermo Reyes, PhD

Author: greyessouto