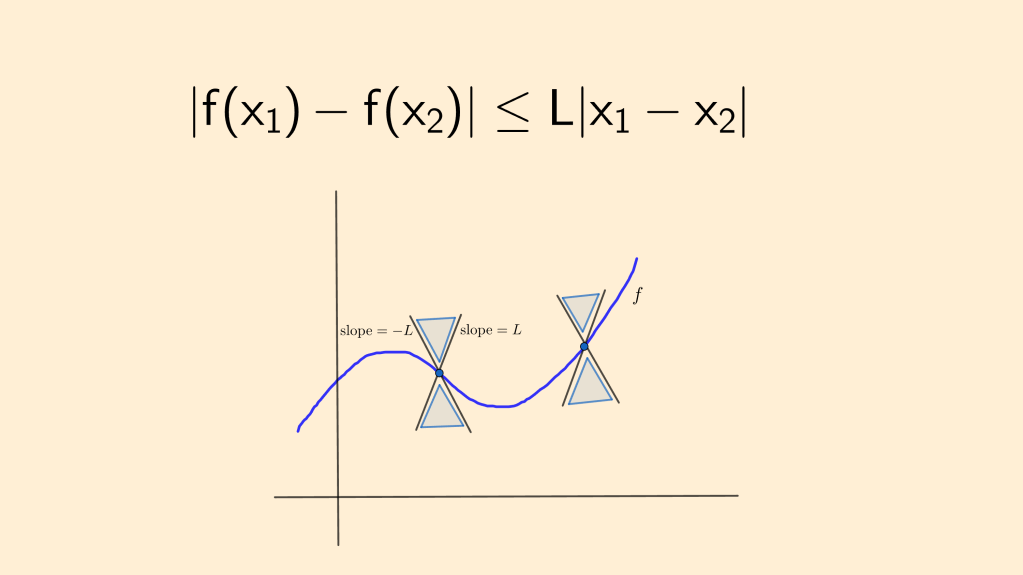
The Lipschitz condition and uniqueness for ODEs

/ greyessouto

Fig.1. (L) The Lipschitz condition for a function f. (R) Rudolph Lipschitz (1832 -1903)

A classic condition on the right hand side of a first order normal ODE

\displaystyle{\frac{dx}{dt}=f(t,x)}

guaranteeing local uniqueness of solutions with given initial value x(t_0)=x_0 is Lipschitz continuity of f in the x variable in some open, connected neighborhood U of (t_0,x_0) where f is defined. That is, it is required that there exist some constant L>0 such that

|f(t,x_1)-f(t,x_2)|\le L|x_1-x_2|,\qquad\qquad\qquad \textrm{(LC)}

for all (t,x) in U. Under the above condition there is a unique local solution of the initial value problem

\left\{\begin{array}{l}\displaystyle{ \frac{dx}{dt}=f(t,x)} ;\\[10pt] x(t_0)=x_0 \end{array}\right.\qquad\qquad\qquad \textrm{(IVP)}

where uniqueness means that two prospective solutions defined on open intervals containing t_0 coincide in their intersection. We assume that our solutions are classical, \it{i.e.}, continuously differentiable. Such solutions exist when extra conditions on f are imposed. For instance, if f is assumed continuous in U, classical local solutions exist and can be extended up to the boundary of U. But here our concern is uniqueness.

My goal here is to explain why such condition implies uniqueness in simple terms, how it can be generalized and the relation between uniqueness and another interesting phenomenon, namely finite-time blow-up of solutions.

To illustrate the idea, we will assume that t_0=0 and x_0=0. We will also assume that f(t,0)=0 for every t and, therefore, one solution of the above IVP is x(t)\equiv 0. The general case reduces to this one, as we explain later.

We focus on forward uniqueness. Namely, we will prove that a solution x(t) with x(t_1)=x_1\neq 0 for some t_1>0 can never be zero at t=0. We will assume x_1>0, as the case x_1<0 can be handled in a similar way. Backwards uniqueness also follows easily from the forward result.

Uniqueness is violated if, as t decreases from t_1 to zero, x(t) vanishes at some point \bar t, 0\le \bar t<t_1, while x(t)>0 for \bar t<t\le t_1. By the Lipschitz condition,

|f(t,x(t))|=|f(t,x(t))-f(t,0)|\le L x(t)

while x(t)>0. It then follows from the ODE that

\displaystyle{\frac{dx}{Lx}\le dt}

along the solution for t\in (\bar t,t_1). Integrating this inequality over [t,t_1],

\displaystyle{t_1-t\ge\frac{1}{L}\int\limits_x^{x_1}\frac{ds}{s}}\qquad\qquad\qquad\textrm{(II)}

This integral inequality is the crux of the argument. Just observe that, since the improper integral is divergent, x(t) approaching zero would require t\to -\infty, contradicting the assumption x(t)\to 0 as t\to \bar t^+. The Lipschitz condition prevents x(t) from becoming zero over finite t-intervals.

The argument above is equivalent to the following: for any solution x(t) with x(t_1)=x_1>0 for some t_1>0 one can construct an exponential barrier from below of the form y(t)=Ce^{Lt} for some C>0, that is, x(t)\ge Ce^{Lt} for all t<t_1 in its domain, thus preventing x(t) from becoming zero. Indeed, the inequality

\displaystyle{\frac{dx}{dt}}\le Lx

implies that our solution x(t) is increasing at a slower pace than the solution y(t) of the IVP

\left\{\begin{array}{l}\displaystyle{ \frac{dy}{dt}=Ly} ;\\[10pt] y(t_1)=x_1 \end{array}\right.

which is nothing but y(t)=Ce^{Lt} for the appropriate C>0. Therefore, y(t)\le x(t) to the left of t_1. In other words, y(t) acts as a lower barrier for x(t), as in the figure below.

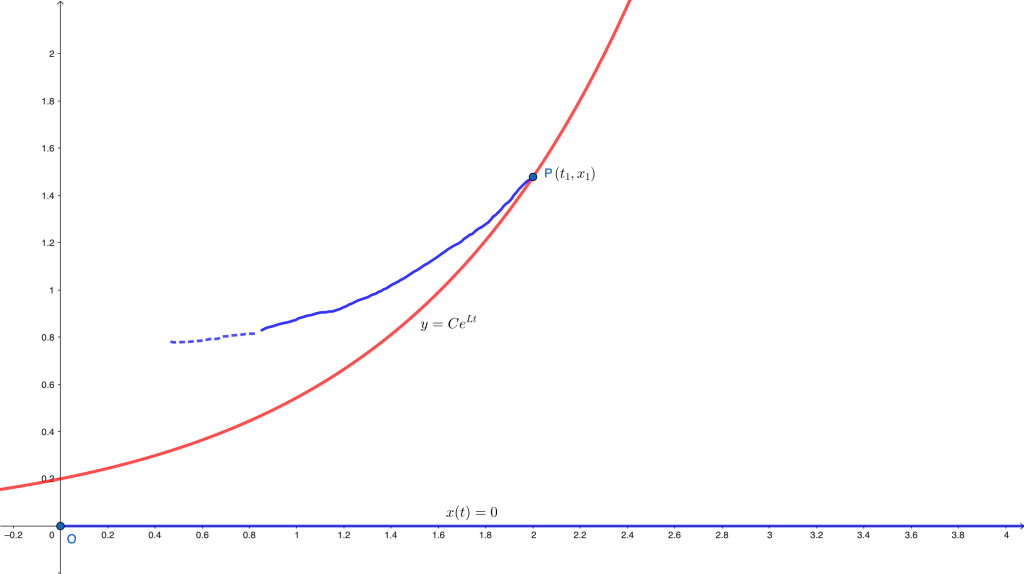
Fig 2. The exponential barrier prevents the solution through P from reaching the t-axis.

If we assume that x_1<0, we use the inequality (again a consequence of \textrm{(LC)})

\displaystyle{\frac{dx}{dt}}\ge Lx

for x<0 to conclude that y(t)=De^{Lt} with D<0 is a barrier from above for our solution, preventing it from reaching the t-axis.

The integral inequality \textrm{(II)} suggests a very natural generalization. Indeed, all we need is a diverging (at zero) improper integral on the right-hand side. We can replace the Lipschitz condition by the existence of a modulus of continuity, that is a continuous function \Phi: [0,\infty)\to [0,\infty) with \Phi(0)=0, \Phi (u)>0 for u>0 satisfying

|f(t,x_1)-f(t,x_2)|\le \Phi(|x_1-x_2|)

in U, with the additional property

\displaystyle{\int\limits_{0^+}\frac {ds}{\Phi(s)}=\infty}.

This more general statement is due to W. Osgood. The Lipschitz condition corresponds to the choice \Phi(s)=s. The proof is identical to the one above, given that the only property we need is the divergence of the improper integral of 1/\Phi at 0^+.

Thus, for an alternative solution to branch out from the trivial one, we require a non-Lipschitz right-hand side in \textrm{(IVP)} that leads to a convergent improper integral. This condition is satisfied, for instance, in the autonomous problem

\left\{\begin{array}{l}\displaystyle{ \frac{dx}{dt}=x^{2/3}} ;\\[10pt] x(0)=0 \end{array}\right.

which, apart from the trivial solution, has solutions of the form x(t)=0 on [0,c) and x(t)=(t-c)^3/27 for t\ge c for any c>0.

There is nothing special about the power 2/3 in this example. Any power \alpha with 0<\alpha<1 would do. These examples of non-uniqueness are usually attributed to G. Peano.

Uniqueness for general solutions can be easily reduced to the special case above. Namely, if \hat x(t) and x_1(t) are local solutions of \textrm{(IVP)} (say on [t_0,t_1)), then \bar x(s)=\hat x(t_0+s)-x_1(t_0+s) is a local solution of

\left\{\begin{array}{l}\displaystyle{ \frac{d\bar x}{ds}=g(s,\bar x):=f(s+t_0, \bar x+x_1(s+t_0))-f(s+t_0, x_1(s+t_0))} ;\\[10pt] \bar x(0)=0 \end{array}\right.

on [0,t_1-t_0) with g(s,0)= f(t, x_1(t))-f(t,x_1(t))=0. Moreover, g satisfies a Lipschitz condition near (s,\bar x)=(0,0) if f does near (t_0,x_0), with the same constant L. By the above particular result, \bar x(s)\equiv 0 and hence \hat x(t)\equiv x_1(t) on the corresponding intervals.

Remarks: a) A simple and widely used sufficient condition for \textrm{(LC)} to hold is the continuity of the partial derivative \displaystyle{\frac{\partial f}{\partial x}} in an x-convex region U (typically a rectangle). This follows from a straightforward application of Lagrange’s mean value theorem; b) \textrm{(LC)} is not necessary for uniqueness, as the example of \textrm{(IVP)} with f(t,x)=x^{\alpha}\sin\frac 1{x} with \alpha\in (0,2] shows; d) The Lipschitz condition is relevant in other areas of Analysis. For instance, it guarantees the uniform convergence of Fourier series.

A related phenomenon: blow up in finite time.

Local solutions issued from (t_0,x_0) can be extended to the boundary of U, but not necessarily in the t-direction. The reason is a fast (superlinear) grow of f(t,x) as x\to\pm\infty, assuming that the domain of definition of f extends indefinitely in the x-direction. A simple example is the problem

\left\{\begin{array}{l}\displaystyle{ \frac{dx}{dt}=x^2} ;\\[10pt] x(t_0)=x_0>0 \end{array}\right.,

whose explicit solution \displaystyle{x(t)=\frac{x_0}{1-x_0(t-t_0)}} “blows up” as t\to (t_0+1/x_0)^-, despite the fact that f(x,t)=x^2 is smooth on the whole plane. The role of the superlinear growth at infinity is similar to the role of Lipschitz (or Osgood) condition in bounded regions for uniqueness. The above problem is equivalent to

\displaystyle{\int\limits_{x_0}^x\frac{dx}{x^2}=t-t_0}

Convergence of the improper integral \displaystyle{\int\limits^{\infty}\frac{dx}{x^2}} prevents t from attaining arbitrarily large values. Calling \displaystyle{T=t_0+\int\limits_{x_0}^{+\infty}\frac{dx}{x^2}=t_0+1/x_0}, we have \lim_{t\to T^-}x(t)=+\infty. This phenomenon is called finite time blow-up and is exhibited by ODEs with superlinear right-hand-sides, by some evolution PDEs with superlinear sources, etc.

The same reasoning applies in the general case when there exists a continuous \Psi>0 such that f(t,x)>\Psi(x) as x\to\infty (resp. f(t,x)<-\Psi(x) as x\to-\infty) if only

\displaystyle{\int\limits^{\infty}\frac{ds}{\Psi(s)}<\infty,\quad\textrm{resp.}\quad\int\limits_{-\infty}\frac{ds}{\Psi(s)}<\infty}.

This time, under assumptions guaranteeing existence and uniqueness of solutions and provided the first condition above holds, the (forward) solution to \textrm{(IVP)} with x(t_0)=a>0 stays to the left of the solution of

\left\{\begin{array}{l}\displaystyle{ \frac{dx}{dt}=\Psi(x)} \\[10pt] x(t_0)=x_0 \end{array}\right.

with 0<x_0<a. The latter blows up in finite time, namely at time \displaystyle{T=t_0+\int\limits_{x_0}^{\infty}\frac{ds}{\Psi(s)}}, forcing the solution to our IVP to blow up at some T'\le T.

Leave a comment